|
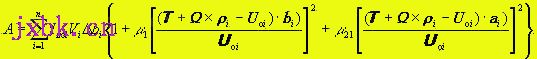 (8) (8)
这里T和Ω是两个状态参数(向量),需要按最小能量原理来确定。为此,令A/T=0和A/Ω=0,导出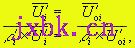 (9) (9)
这里Ui′和Uoi′分别是诱导排屑向量与诱导自然排屑向量(图2,图中标注的文字均略去了下标“i”),
Ui=μ1Uitbi+μ2Uinai;
Uoi=μ1Uoitbi+μ2Uoinai.(10)
(9)式中上横线表示加权平均,即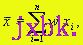 (11) (11)
以各单元刀具在自由切削下的单元主切削功率为权,归一化的权系数为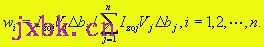 (12) (12)
如果有一对Tm和Ωm确实使切削功率A取极小值,那么,(9)式必须满足。另一方面,(9)式又提供了一种计算Tm和Ωm的途径。此式概括了按最小能量原理确定状态参数的一般规则。
将算出的Tm和Ωm代入(8)式,即得实际的、受到最小能量原理支配的切削功率Amin。
2 非自由切削实例分析
作者已给出许多实验事实,表明了(9)式所示的一般原则,在各种具体的条件下的应用及其正确性。这里不拟讨论该式的一般求解方法,及Tm和Ωm的一般计算方法问题,在此仅以圆弧刃刀具成形车削为例,来说明基于最小能量原理对于非自由切削过程的分析方法。用于实验和分析的刀具如图3所示。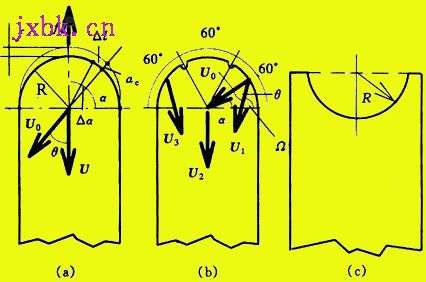
图3 用于实验和分析的圆弧刃刀具
横向切入车削,工件:紫铜,刀具:高速钢,γoi=λsi=0°。
(a) 凸圆弧刃,不带分屑槽; (b) 凸圆弧刃, 带分屑槽; (c) 凹圆弧刃
2.1 单元刀具非线性综合法
首先,由单元刀具切削试验,可拟合出关于单位长度刀刃上主切削力的经验公式,
I=1593ac0.61(1+0.76θ2)(13)
此式是进一步分析的依据。式中,θ为受迫排屑方向偏离自然排屑方向的角度。
假定诸单元刀具均能沿径向(即各单元刀具的自然排屑方向)排屑,即令上式中θ=0°,长度为Δl的单元刀具上的单元主切削力为
ΔFzo=1593a0.61cΔl,(14)
而如图3(a)所示刀具的主切削力即为各单元刀具上的单元主切削力之和,
|


