由于粉末冶金技术、模具制造技术、及数控刃磨技术的高度发展,现代金属切削刀具的切削部分已可做成十分复杂的形状,其切削过程也十分复杂。一把真实的金属切削刀具,可视为一系列单元刀具的组合。研究表明,单元刀具的排屑向量(包括排屑方向与排屑速度)的自然取值总是使切削功率趋于极小,此即所谓单元刀具切削下的最小能量原理。
在切削过程中,诸单元刀具并行地进行切削,各自都力图按其自然排屑向量排出切屑。这些“各行其是”的排屑向量势必相互干涉和冲突;而为了维系各单元刀具所排出共同切屑的整体性,诸单元刀具又必须相互协调其排屑向量,以确定整体的排屑运动。研究表明,制约整体排屑运动的自然法则仍然是“最小能量原理”:即在满足由控制参数所设定的约束条件的所有可能的整体的排屑运动中,那个可以实现的整体的排屑运动,必须使整把刀具所消耗的切削总功率(即诸单元刀具所消耗的切削功率之和)取极小值。
因存在排屑干涉而必须进行排屑协调的切削过程称为“非自由切削”。几乎所有的实际切削加工工序都属于非自由切削。在非自由切削过程中,最小能量原理保证了整把刀具的切削能耗最小,但无法使每个单元刀具的实际排屑向量都与其自然排屑向量一致。事实上,经过排屑协调以后,一般来说,每个单元刀具都不得不作出适当的让步,而不能按其自然排屑向量排屑。于是,一把刀具切削的总功率,往往大于其所包含的全部单元刀具各自单独工作时的能耗之和。这体现了非自由切削过程的强烈的非线性特征。这一特征使得切削能耗上升;切屑变形复杂化,加工表面光洁度恶化;切削力上升,工艺系统的变形增加,加工精度下降;切削温度升高,刀具寿命缩短,停车换刀时间增加,效率下降,成本增加。现代切削加工中的许多问题,往往源于非自由切削的这些弊端。
本文提出了一种“单元刀具综合法”,用以解释、预测和优化形状复杂刀具的切削性能。与前人所采用的方法相比,本文所提出的方法的特点在于它基于“最小能量原理”,妥善地处理了复杂刀具的切削过程中的排屑干涉及由此引起的非线性问题。
1 非自由切削过程总体排屑运动的一般规律
1.1 单元刀具的划分与描述
设一把刀具被沿其刀刃划分成一系列单元刀具(图1)。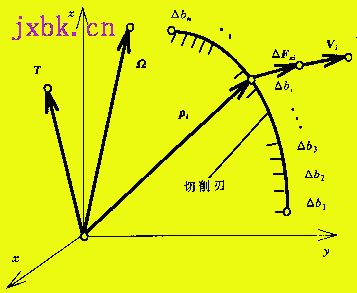
图1 切屑的总体运动与单元刀具的划分
各单元刀具的位置向径ρi,刀刃方向的单位向量bi,前刀面内垂直于刀刃的单位向量ai(图2),刃长Δbi,主要几何参数γoi,λsi和切削用量aci,Vi(i=1, 2, …, n),可通过对刀具进行几何分析和运动分析来获得。第i个单元刀具单位长度刀刃上的主切削力
Izoi=Izoi(γoi, λsi, aci, Vi)(i=1,2, …,n)(1)
和自然排屑向量
Uoi=Uoi(γoi, λsi, aci, Vi)(i=1,2,…,n)(2)
图2 排屑向量
Uo为自然排屑向量,U为实际排屑向量,
U′为诱导排屑向量
可通过对于单元刀具的实验研究或理论分析来获得(影响主切削力和自然排屑向量的,还有工件与刀具材料、冷却润滑条件等因素,但对于同一把刀具的所有单元刀具来说,这些因素都是相同的,即可视为恒量,因此在以上两式中未予表示)。Uoi可按平行、或垂直于刀刃方向分解为(图2)
Uoit=Uoi.bi, Uoin=Uoi.ai.(3)
根据单元刀具排屑的最小能量原理,整个刀具的功率消耗可表示为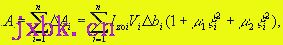
式中ζi与ξi分别是U在平行于及垂直于刀刃方向对于Uo的相对变动量(图2),
ζi=ΔUit/Uoi=(Uit-Uoit)/Uoi,
ξi=ΔUin/Uoi=(Uin-Uoin)/Uoi,(5)
而系数μ1和μ2分别表示ζi和ξi对于切削功率的影响强度。
1.2 切屑的整体运动
切屑在前刀面上一旦形成,它作为一个整体的运动可视为刚体运动(弹性变形略而不计)。如所周知,刚体运动由一个平移T和一个旋转Ω组成(图1),而位置向径为ρi的单元刀具处的实际排屑向量为
Ui=T+Ω×ρi, i=1, 2, …, n(6)
它可以分解为
Uit=Ui.bi, Uin=Ui.ai(7)
1.3 最小能量原理
将(5)~(7)式代入(4)式, |


