例三  环面蜗杆
我们可以假象此蜗杆由车刀车成，此车刀的切削刃在草图平面上，在车削过程中车刀绕一固定点转动，其转动速度与蜗杆转动速度相适应（按定比速率转动），草图平面通过蜗杆轴。
显然，路径是一个螺旋线，但是不能是一个变径或变距的螺旋线，因为从前面基本概念中知道，在扫描过程中轮廓平面与路径切线的相对位置不变，以变径或变距的螺旋线为路径必将破坏轮廓平面通过蜗杆轴线的条件。幸好我们前面已知道路径可以只是个驱动器，实际的轮廓运动形态可由引导线来控制。
为了保证轮廓在草图平面中绕一个中心转动，我们可以作一个垂直于蜗杆轴线的圆为引导线，该圆的中心在蜗杆轴上，当我们将轮廓的转动中心作为引导线的穿透点时，该轮廓的转动中心在蜗杆的轴向位置被固定。
还有一个关键问题是怎样将轮廓的转动与扫描过程建立一个联系，让我们来看一下轮廓草图





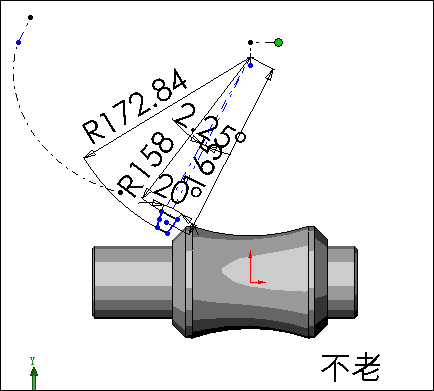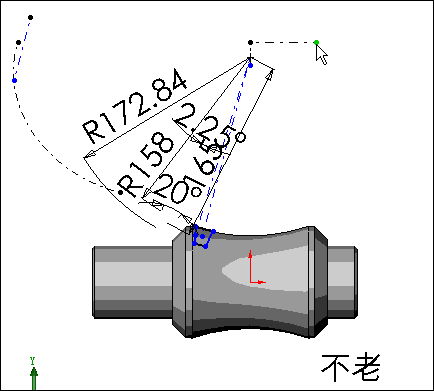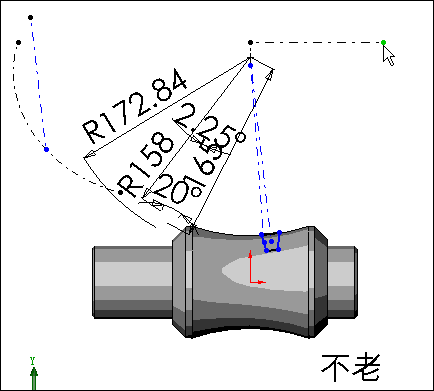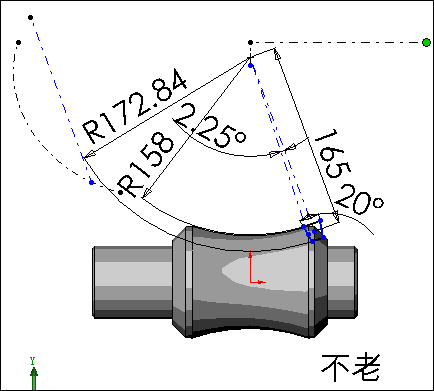
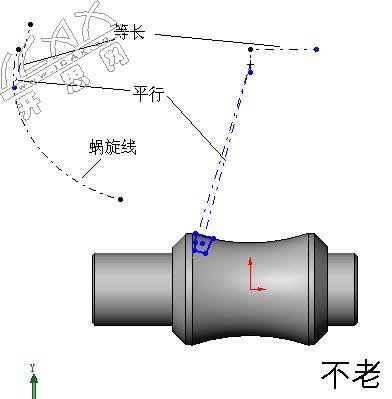
从图中我们看到在扫描过程中，轮廓及其转动中心受引导线约束不动，被鼠标拉动的一点随着螺旋扫描路径向前移动，在等长约束的作用下蜗旋线有一个线段也在移动，再利用平行约束条件带动扫描轮廓转动。因为蜗旋线处的线段长度与转角成正比，因此保证了扫描轮廓草图平面随螺旋线路径的转动与轮廓在草图平面内的转角呈正比关系。
注意：
1、蜗旋线是螺旋运动转换成转角的转移器；
2、引导线可以是闭合的，它相当于一条无限长的引导线。

例四  渐开线
渐开线有用放样方法制作，比用扫描方法简洁，此处用扫描方法只是便于理解挪移心法而已。
由于用渐开线定义作图，其轮廓、基圆、及作图平面必须在同一平面上，所以路径必须与该平面相交，可以采用螺旋线或垂直于轮廓平面的直线，此处路径采用较简单的后一种路径。
本渐开线基圆直径100，引导线是由基圆生成的带有外张锥度的螺旋线，螺旋线外张的角度使当一点沿螺旋线转一周时该点径向外移100×π。


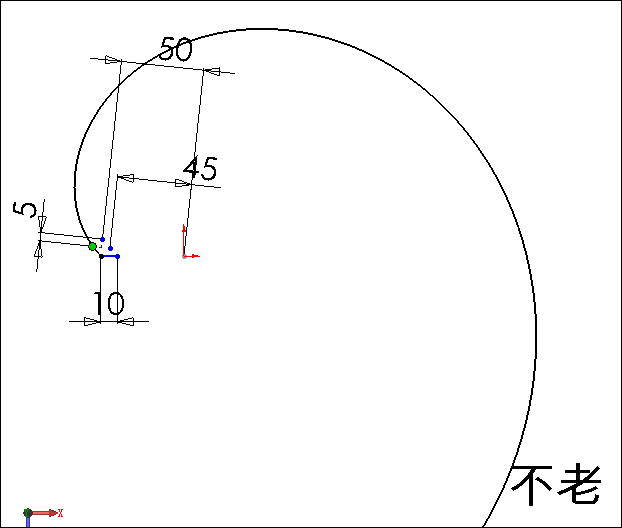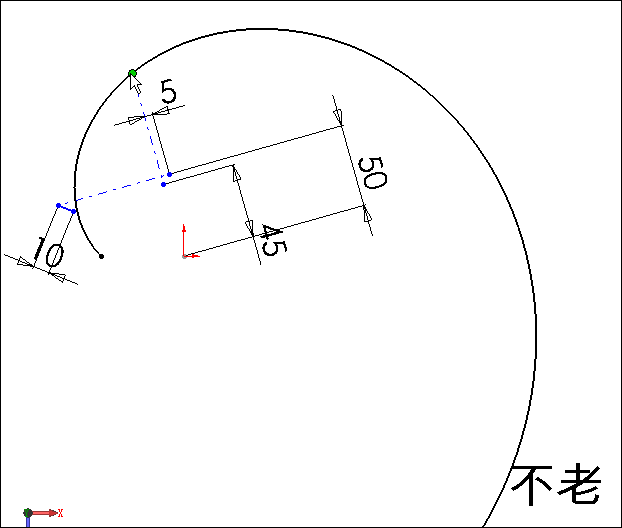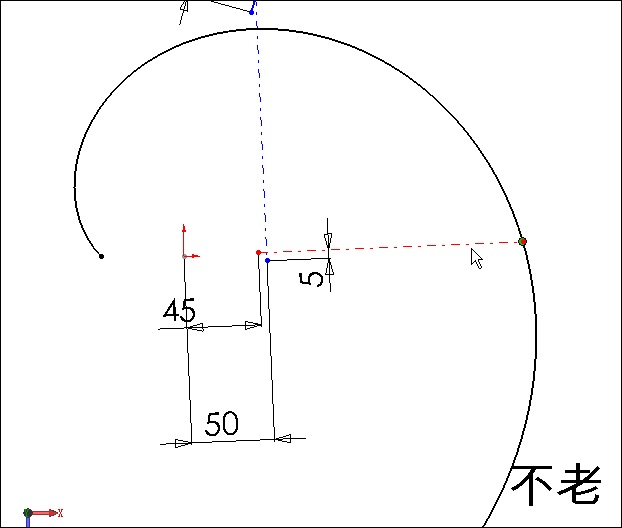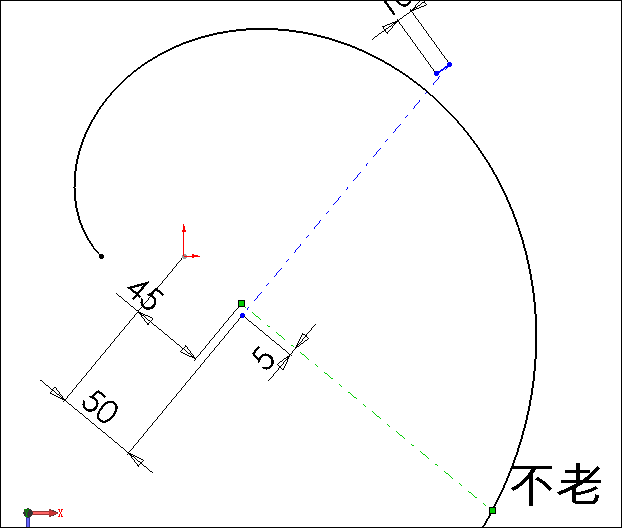
在草图中可以看出当穿透点沿螺旋线移动时，该点在草图平面按蜗旋线方式移动，其螺距为100×π，因此该点在移动过程中的径向增量与移过的基圆弧长相等，图中我们在切线和螺旋线径向增量之间添加有一个等长约束，显见切线长等于基圆弧长，这就是渐开线的定义。
注意到在反映螺旋线径向增量值和切线长度值的线段处各增长了5mm，是为了避免在初始点出现零长度的线段。
扫描作出的是一个三维曲面，其外边线在上视面的投影即是渐开线。
注意：
1、在带有外张锥度的螺旋线上运动的穿透点具有轴向、径向、切向移动皆成正比的特性，是一个很理想的转移器，
2、要尽量避免产生零长度的线段，否则容易产生扫描失败，或扫描不稳定现象
例五  摆线齿轮
在这里，我们作的是一个短肢外摆线，见下图