| 柔性制造系统刀具需求规划问题的研究 |
|
| 日期:2007-8-20 21:28:50 人气:73 [大 中 小] |
|
|
|
|
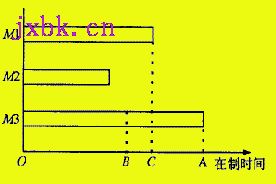
图1 算法迭代示意图
4 规划中央刀具库配置的启发式算法
本节介绍的启发式算法就是逐步增加关键机床上的关键刀具的数量,所谓关键机床就是指所有机床中最后一个加工完工件的机床,所为关键刀具就是指“刀具的等待时间之和/刀具成本”最大的刀具。算法的重复执行过程可以用图1来描述。假定机床3在当前这一步是关键机床,任务的在制时间在A点结束,那么在初始中央刀具库状态中增加机床3加工过程中关键刀具的数量,重新计算任务的在制时间和关键机床,并确定关键机床上的关键刀具。假设机床3在B点结束,这一步任务的在制时间在C点结束,机床1变成了关键机床,则在初始中央刀具库中增加机床1加工过程中的关键刀具的数量,依此类推。整个过程不断重复,直到超过允许的刀具购买资金。本文的算法综合了一些其它文献的思想。
本文仅研究刀具需求规划问题。虽然工件调度对在制时间影响很大,但这是一个非常复杂的问题。我们可以认为在制时间由两部分组成:一部分由工件调度引起,另一部分由刀具配置引起。性能最好的工件调度策略可以通过比较来选择,但这不是本文的重点。在以后的描述中,我们均假定工件调度策略已经确定。
令B为允许的刀具购买资金,Ci为刀具规格i的购买价格。则规划中央刀具库配置的算法(算法2)如下:
step1 ni=1,对所有iÎ W,B'=B-SCiiÎ W;
step2 采用算法1求的关键机床(如果有多台关键机床,任意取其中一台作为关键机床),记为c,同时得到Ajc和djc," j Î Oc;
step3 令i=1;
step4 令j=1,xi=0;
step5 如果 i ÎAjc,则xi=djc+xi;
step6 j=j+1,如果j≤|Oc|,转Step5;
step7 i=i+1,如果i≤|W|,转step4;
step8 按xi/Ci非递增的顺序排列得到刀具序列t1,t2,…,t|Oc|;
step9 令k=1
step10 如果Ctk£ B',则ntk=ntk+1,B'=B'-Ctk,转Step2;
step11 k=k+1,如果k > |W|,停止。否则,转Step10;
5 计算结果与比较
计算环境如下:机床数4~8,工件数目30~80,每个工件所需得刀具规格数30~50,刀具规格总数50~100,每个工件的执行时间50~100,每种规格刀具的价格10~100,使用寿命为2000~3000,每台机床的机床刀具库容量固定为60,允许的刀具购买资金预算取任务所需的最小刀具成本的1.5倍,最小刀具成本就是当在制时间不为无穷大时任务所需的最小刀具集合的成本。 |
|
|
| 我有问题,我要进入论坛 |
| 出处:本站原创 作者:佚名 | |
|


